In early June, we announced a significant achievement with LFortran: the Fastest Open-Source Compiler in Compile-Time Evaluation of an Array Benchmark. Continuing our commitment to performance enhancement, we are pleased to announce that LFortran now includes support for OpenMP pragmas and parallelizing do concurrent. Particularly for parallel do OpenMP construct, our implementation is fully operational and achieves performance comparable to GFortran.
Note that LFortran is still a alpha software, meaning that users must continue expecting that LFortran will fail compiling or running their codes. Please report all bugs that you find.
Compilation Benchmark
Matrix Multiplication example
Let us now take a look at matrix multiplication using OpenMP
subroutine matrix_multiplication(l, m, n)
use omp_lib
integer :: l, m, n, i, j, k
integer :: seed
double precision :: a(l, n), b(l, m), c(m, n)
double precision :: start_time, end_time
seed = 123456789
b = 121.124D0
c = 29124.012D0
start_time = omp_get_wtime()
!$omp parallel do shared(a, b, c, l, m, n)
do j = 1, n
do i = 1, l
a(i,j) = 0.0D+00
do k = 1, m
a(i,j) = a(i,j) + b(i,k) * c(k,j)
end do
end do
end do
!$omp end parallel do
end_time = omp_get_wtime()
print *, "Time: ", end_time - start_time
print *, "sum(a): ", sum(a)
end subroutine
program openmp_30
call matrix_multiplication(500, 500, 500)
end program
Let’s benchmark different matmul sizes for 8 threads:
GFortran (fast) : -O3 -march=native -ffast-math -funroll-loops
| L=M=N | GFortran | GFortran (fast) | LFortran (–fast) | GFortran (fast) / LFortran (–fast) |
|---|---|---|---|---|
| 500 | 0.078481 | 0.021822 | 0.024509 | 0.890369 |
| 1000 | 0.706202 | 0.191768 | 0.188653 | 1.016512 |
| 1500 | 2.418719 | 0.691059 | 0.695324 | 0.993866 |
| 2000 | 5.889707 | 1.845945 | 1.885804 | 0.978864 |
| 3000 | 24.358390 | 9.179583 | 8.565501 | 1.071692 |
| 4000 | 84.909953 | 37.292557 | 40.427580 | 0.922453 |
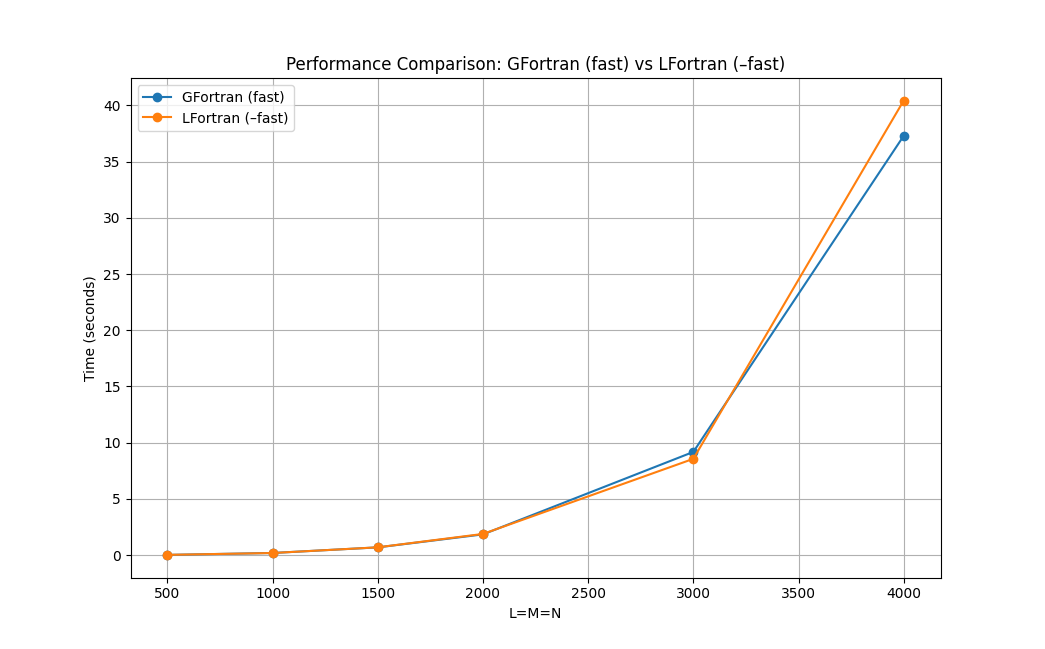
Now let’s benchmark strong scaling with a given matmul shape L=M=N=4000:
| Num Threads | GFortran (fast) | LFortran (–fast) | GFortran (fast) / LFortran (–fast) |
|---|---|---|---|
| 1 | 144.339067 | 147.331973 | 0.979686 |
| 2 | 76.052912 | 77.598491 | 0.980082 |
| 4 | 45.320663 | 47.642641 | 0.951263 |
| 8 | 33.889175 | 39.491259 | 0.858144 |
| 16 | 35.262666 | 40.834357 | 0.863554 |
| 32 | 35.644130 | 40.365258 | 0.883040 |
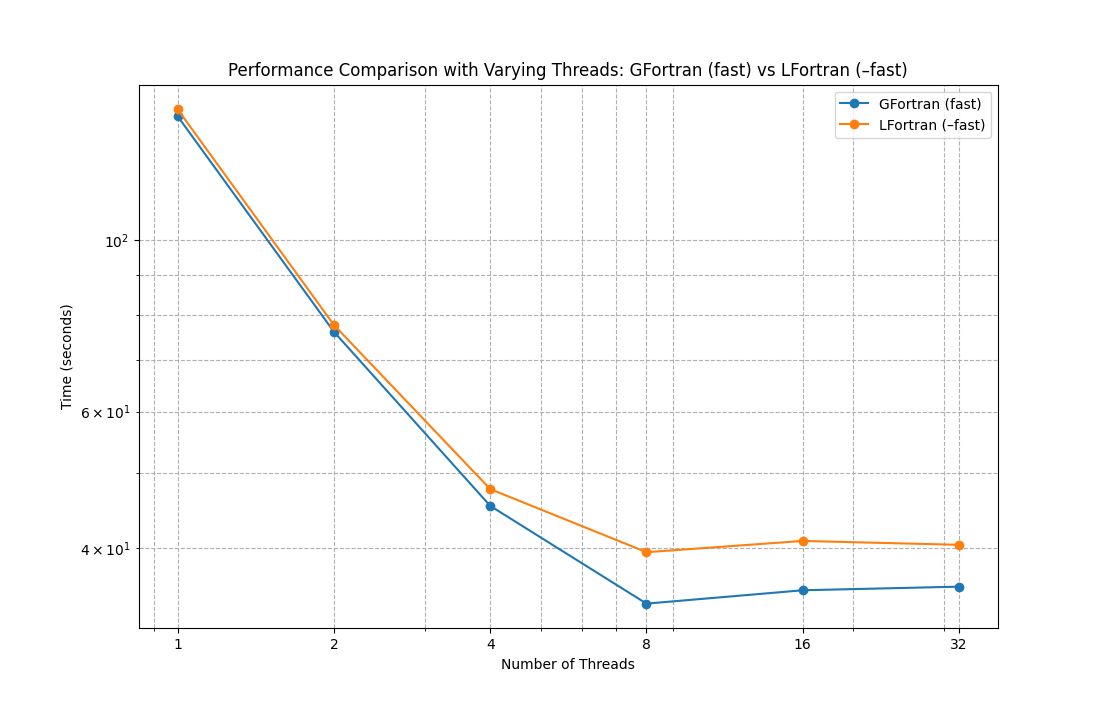
From the benchmarks and plot we can see that LFortran is competitive with GFortran when it comes to runtime performance. Both compilers run in parallel with the performance as expected: almost linear speedup up to about 4 threads, and plateauing beyond that due to the IO bottleneck.
Works with do concurrent
Cherry on top, we get the same runtime performance if we use DoConcurrentLoop instead of OpenMP pragmas. We just have to provide sufficient semantic information and that is it.
Matrix Multiplication with do concurrent
! equivalent to above openmp example
subroutine matrix_multiplication(l, m, n)
use omp_lib
integer :: l, m, n, i, j, k
integer :: seed
double precision :: a(l, n), b(l, m), c(m, n)
double precision :: start_time, end_time
seed = 123456789
b = 121.124D0
c = 29124.012D0
do concurrent (j = 1:n) shared(a, b, c, l, m, n)
do concurrent (i = 1:l)
a(i,j) = 0.0D+00
do concurrent (k = 1:m)
a(i,j) = a(i,j) + b(i,k) * c(k,j)
end do
end do
end do
print *, "sum(a): ", sum(a)
if (abs(sum(a) - (440952103687207.56D0)) > 1D-12) error stop
end subroutine
program do_concurrent_12
call matrix_multiplication(500, 500, 500)
end program
This works both with and without openmp flags.
% lfortran do_concurrent_12.f90
sum(a): 4.40952103687207562e+14
% lfortran do_concurrent_12.f90 --openmp --openmp-lib-dir=$CONDA_PREFIX/lib
sum(a): 4.40952103687207562e+14
Mandelbrot example
program mandelbrot
use omp_lib
integer, parameter :: Nx = 600, Ny = 450, n_max = 255, dp=kind(0.d0)
real(dp), parameter :: xcenter = -0.5_dp, ycenter = 0.0_dp, &
width = 4, height = 3, dx_di = width/Nx, dy_dj = -height/Ny, &
x_offset = xcenter - (Nx+1)*dx_di/2, y_offset = ycenter - (Ny+1)*dy_dj/2
real(dp) :: x, y, x_0, y_0, x_sqr, y_sqr, wtime
integer :: i, j, n, image(Nx, Ny)
call omp_set_num_threads(4)
wtime = omp_get_wtime()
!$omp parallel shared(image) private(i, x, y, x_0, y_0, x_sqr, y_sqr, n)
!$omp do
do j = 1, Ny
y_0 = y_offset + dy_dj * j
do i = 1, Nx
x_0 = x_offset + dx_di * i
x = 0; y = 0; n = 0
do
x_sqr = x ** 2; y_sqr = y ** 2
if (x_sqr + y_sqr > 4 .or. n == n_max) then
image(i,j) = 255-n
exit
end if
y = y_0 + 2 * x * y
x = x_0 + x_sqr - y_sqr
n = n + 1
end do
end do
end do
!$omp end do
!$omp end parallel
wtime = omp_get_wtime() - wtime
print *, 'Time = ', wtime, "(s)"
print *, sum(image)
end program
% lfortran mandelbrot.f90 --openmp --openmp-lib-dir=$CONDA_PREFIX/lib
Time = 1.75323009490966797e-01 (s)
59157126
Mandelbrot example using do concurrent
program mandelbrot_do_concurrent
integer, parameter :: Nx = 600, Ny = 450, n_max = 255, dp=kind(0.d0)
real(dp), parameter :: xcenter = -0.5_dp, ycenter = 0.0_dp, &
width = 4, height = 3, dx_di = width/Nx, dy_dj = -height/Ny, &
x_offset = xcenter - (Nx+1)*dx_di/2, y_offset = ycenter - (Ny+1)*dy_dj/2
real(dp) :: x, y, x_0, y_0, x_sqr, y_sqr, wtime
integer :: i, j, n, image(Nx, Ny)
do concurrent (j = 1:Ny) shared(image) local(i, x, y, x_0, y_0, x_sqr, y_sqr, n)
y_0 = y_offset + dy_dj * j
do i = 1, Nx
x_0 = x_offset + dx_di * i
x = 0; y = 0; n = 0
do
x_sqr = x ** 2; y_sqr = y ** 2
if (x_sqr + y_sqr > 4 .or. n == n_max) then
image(i,j) = 255-n
exit
end if
y = y_0 + 2 * x * y
x = x_0 + x_sqr - y_sqr
n = n + 1
end do
end do
end do
print *, sum(image)
end program
As stated above, this works with and without --openmp
% lfortran mandelbrot_do_concurrent.f90
59157126
% lfortran mandelbrot_do_concurrent.f90 --openmp --openmp-lib-dir=$CONDA_PREFIX/lib
59157126
Let’s now do a comparative analysis:
For n_max = 1255
GFortran (fast) : -O3 -march=native -ffast-math -funroll-loops
| num threads | GFortran (fast) | LFortran (–fast) | GFortran (fast) / LFortran (–fast) |
|---|---|---|---|
| 1 | 0.124 | 0.125 | 0.990 |
| 2 | 0.065 | 0.066 | 0.990 |
| 4 | 0.065 | 0.066 | 0.985 |
| 8 | 0.045 | 0.046 | 0.991 |
| 16 | 0.028 | 0.028 | 0.994 |
| 32 | 0.022 | 0.022 | 1.004 |
| 64 | 0.022 | 0.022 | 1.010 |
One has to note that LFortran can get even faster if you first compile to LLVM, then use clang, and enable -ffast-math, which we are not doing at the moment: lfortran --fast should be roughly equivalent to Clang’s -O2, without -ffast-math. If you know how to enable equivalent LLVM optimizations in the LFortran’s driver, please let us know or send us a PR.
How to run benchmark yourselves?
You may install latest GFortran, LFortran or any compiler using conda / mamba and then test it locally.
The following commands will help you create a conda environment with latest versions of LFortran and GFortran installed.
conda create -n omp lfortran=0.37.0 gfortran llvm-openmp
conda activate omp
To test with LFortran one may use:
lfortran file_name.f90 --openmp --openmp-lib-dir=$CONDA_PREFIX/lib
and for GFortran
gfortran file_name.f90 -fopenmp && ./a.out
Development Overview
We added two flags that need to be enabled to fully run an example: --openmp and --openmp-lib-dir=<path-to-omp-library>.
Parser
To incorporate OpenMP pragmas in our Abstract Syntax Tree (AST), we expanded the existing pragma_type node by introducing OMPPragma. Building upon our previous proof of concept with LFortranPragma, we extended its capabilities to include OMPPragma. Subsequently, we modified the parser to recognize and interpret this new pragma type.
For the simple example:
!$omp parallel shared(b, n) private(i) reduction(+:res)
!$omp do
...
!$omp end do
!$omp end parallel
We create an AST node as shown below:
(Pragma
0
OMPPragma
.false.
"parallel"
[(String
"shared(b, n)"
)
(String
"private(i)"
)
(String
"reduction(+:res)"
)]
()
)
(Pragma
0
OMPPragma
.false.
"do"
[]
()
)
...
(Pragma
0
OMPPragma
.true.
"do"
[]
()
)
(Pragma
0
OMPPragma
.true.
"parallel"
[]
(TriviaNode
[]
[(EndOfLine)
(EndOfLine)]
)
)
We have added support for several reduction operations.
reduce_op = ReduceAdd | ReduceSub | ReduceMul | ReduceMIN | ReduceMAX
AST -> ASR
We decided to extend the design of DoConcurrent to support OpenMP features. Therefore, when the --openmp flag is enabled, encountering an OMPPragma will result in the creation of a DoConcurrent loop instead of a DoLoop. This DoConcurrent loop will include sufficient semantic information to facilitate its lowering to the correct API calls in subsequent Abstract Semantic Representation (ASR) passes and the backend.
Thus the grammar of DoConcurrentLoop is as follows
DoConcurrentLoop(do_loop_head head, expr* shared, expr* local, reduction_expr* reduction, stmt* body)
reduction_expr = (reduction_op op, expr arg)
reduction_op = ReduceAdd | ReduceSub | ReduceMul | ReduceMIN | ReduceMAX
Hence, for example:
!$omp parallel shared(b, n) reduction(+:res)
!$omp do
do i = 1, n
res = res + sum(b(i, :))
end do
!$omp end do
!$omp end parallel
The generated ASR looks like:
(DoConcurrentLoop
((Var 3 i)
(IntegerConstant 1 (Integer 4))
(Var 3 n)
())
[(Var 3 b)
(Var 3 n)]
[]
[(ReduceAdd
(Var 3 res))]
[(Assignment
(Var 3 res)
(RealBinOp
(Var 3 res)
Add
(IntrinsicArrayFunction
Sum
[(ArraySection
(Var 3 b)
[(()
(Var 3 i)
())
((ArrayBound
(Var 3 b)
(IntegerConstant 2 (Integer 4))
(Integer 4)
LBound
(IntegerConstant 1 (Integer 4))
)
(ArrayBound
(Var 3 b)
(IntegerConstant 2 (Integer 4))
(Integer 4)
UBound
()
)
(IntegerConstant 1 (Integer 4)))]
(Array
(Real 8)
[(()
())]
DescriptorArray
)
()
)]
0
(Real 8)
()
)
(Real 8)
()
)
()
)]
)
We support nested do loops, pragma inside a do loop at any level of nesting, etc.
ASR -> ASR pass
The real complexity occurs within this ASR-to-ASR pass, where we take the DoConcurrent loop and transform it with the appropriate calls to the corresponding OpenMP C APIs.
We implemented a comprehensive and specialized ASR pass for OpenMP, which efficiently lowers the enhanced DoConcurrentLoop to atomic operations and API calls within the OpenMP library. Our approach involved studying Clang and GFortran’s methodology, understanding their parallelization techniques using calls like GOMP_parallel, and researching atomic operations, critical regions, barriers, and other relevant concepts. Subsequently, we developed logic to ensure accurate translation.
This pass is only run if --openmp flag is enabled.
ASR -> LLVM
With the assistance of the ASR pass, we achieved significant code reduction, enabling our example to work without backend modifications. We observed favorable speedups across threads, indicating successful parallelization of the code.
Runtime library
To support use omp_lib we added bind(C) interfaces to runtime library of LFortran wrapped inside a module. This module gets created as it encounters use omp_lib and is stored in ASR.
Test suite
Up to now, we have successfully implemented and tested approximately 40 OpenMP-related tests, indicating robust functionality across various examples. Despite LFortran being in its alpha stage and the OpenMP pass being a recent addition, we anticipate occasional issues, albeit minor, which can typically be resolved with small adjustments. In addition to these, we replaced OpenMP pragmas with the corresponding do concurrent loops and conducted thorough testing of these implementations.
We even took a real life openmp example from https://fortran-lang.discourse.group/t/openmp-code-implementation-in-gfortran-and-intel/8256 and got it compiled with only a minor fix in the OpenMP ASR pass.
Progress Tracker
We have everything tracked at OpenMP support in AST and ASR and one may filter issues / PRs with label openmp or directly follow link.
Contributing
Help us get to beta faster by reporting bugs and submitting PRs to fix things. We will help you get started, no prior compiler experience needed.
Acknowledgements
We want to thank:
- Sovereign Tech Fund (STF)
- NumFOCUS
- QuantStack
- Google Summer of Code
- GSI Technology
- LANL
- Our GitHub, OpenCollective and NumFOCUS sponsors
- All our contributors (83 so far!)